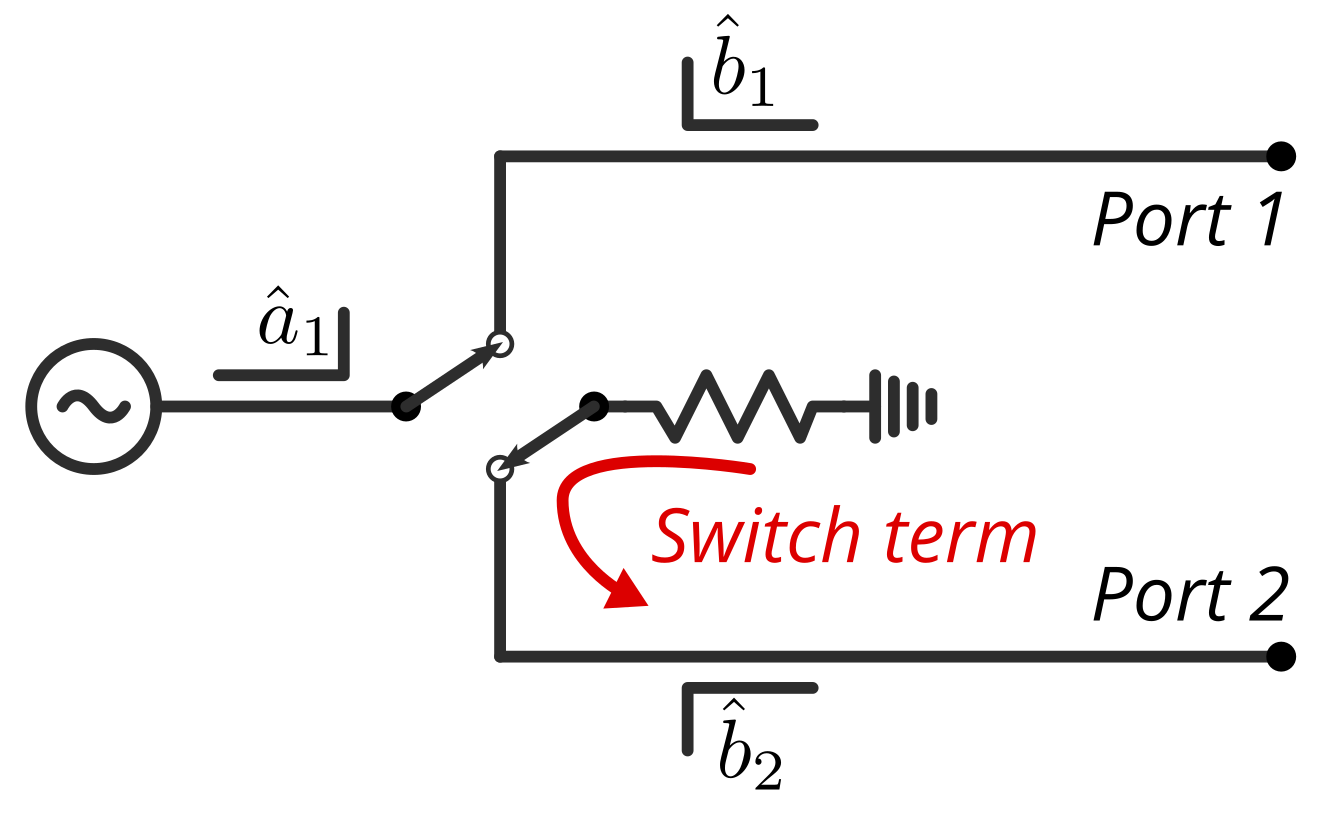
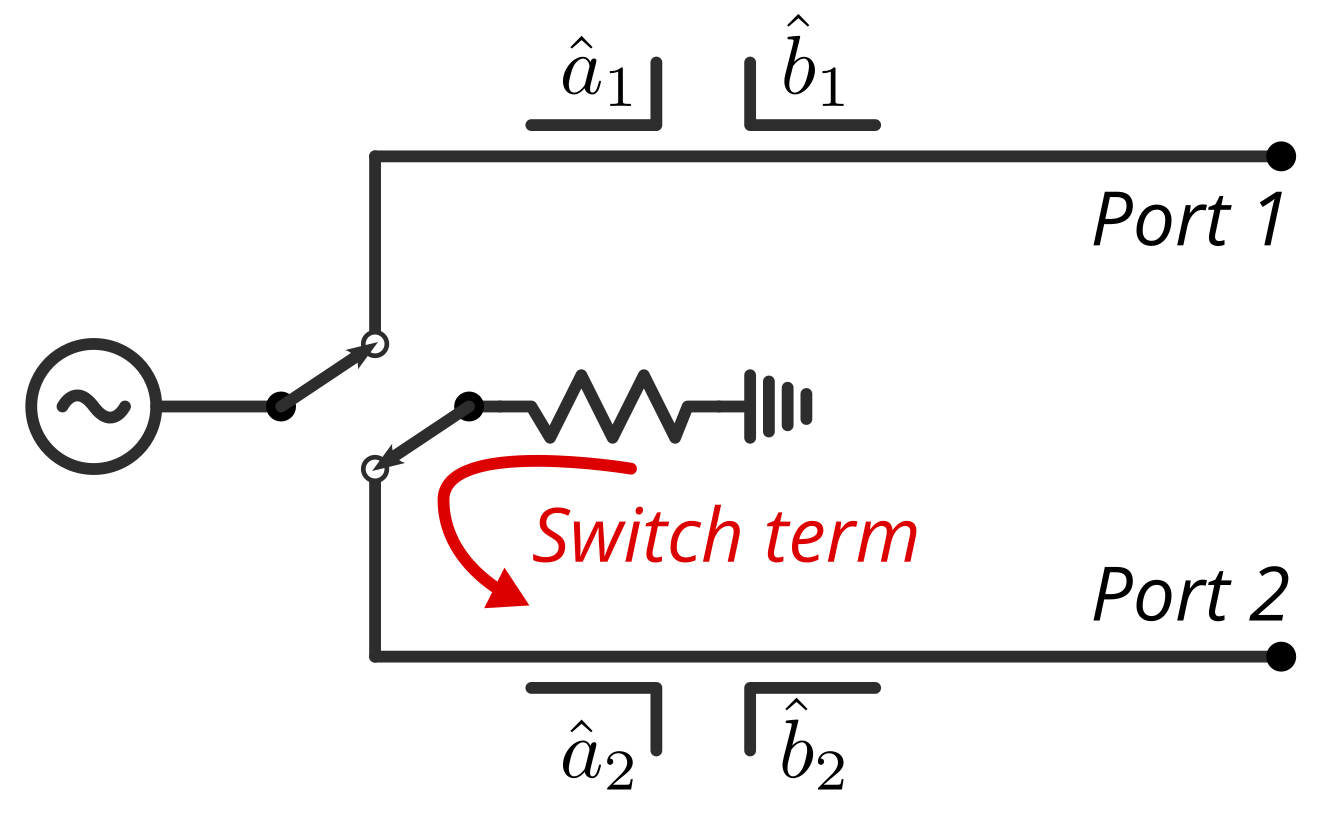
Switch terms are a concept that is often misunderstood in vector network analyzers (VNAs). Although they are essential for VNA calibration, VNA vendors tend not to discuss them in their user manuals. Unlike S-parameters, switch terms cannot be directly selected to display in your VNA. Instead, you must define them yourself using wave parameters.
The purpose of this post is to help you understand the physical meaning of switch terms, explain what they are, and show you how the math is defined. Additionally, I will show you a technique for indirectly measuring switch terms from the VNA using a couple of reciprocal devices [1]. For sample measurements and Python scripts, check my GitHub repository: https://github.com/ZiadHatab/vna-switch-terms
Physical Meaning
To understand the concept of switch terms, let’s start with the basic definition of S-parameters. S-parameters describe a linear transformation between incident and reflected waves, which can be represented by the following matrix equation:
\[\begin{bmatrix} \hat{b}_{1}\\\hat{b}_{2} \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix}\begin{bmatrix} \hat{a}_{1}\\\hat{a}_{2} \end{bmatrix} \label{eq:1}\]where $\hat{a}_i$ and $\hat{b}_i$ represent the incident and reflected waves at port-i, respectively. We can expand this matrix notation into two equations:
\[\hat{b}_1 = S_{11}\hat{a}_1 + S_{12}\hat{a}_2, \qquad \hat{b}_2 = S_{21}\hat{a}_1 + S_{22}\hat{a}_2 \label{eq:2}\]The most common way for solving S-parameters, which is often how S-parameters are taught to many people, involves setting one of the incident waves to zero and solving for the S-parameters as ratios. This is expressed as follows:
\[S_{11} = \left. \frac{\hat{b}_1}{\hat{a}_1}\right|_{\hat{a}_2=0}, \qquad S_{12} = \left. \frac{\hat{b}_1}{\hat{a}_2}\right|_{\hat{a}_1=0}, \qquad S_{21} = \left. \frac{\hat{b}_2}{\hat{a}_1}\right|_{\hat{a}_2=0}, \qquad S_{22} = \left. \frac{\hat{b}_2}{\hat{a}_2}\right|_{\hat{a}_1=0} \label{eq:3}\]In reality, it is not possible to assume that the incident wave of the opposite port is zero. Even if you turn off the source at the other port, the energy that exited the device under test (DUT) can reflect back and enter the DUT. Therefore, from the perspective of the DUT, the energy that enters the non-driving port due to reflection is an incident wave for the DUT. Hence, the idea that you can set, for example, $\hat{a}_2 = 0$ for computing $S_{11}$ is not feasible in practice. See the illustration below.
 Fig. 1. Illustration of exciting wave at port-1 for a two-port DUT.
Fig. 1. Illustration of exciting wave at port-1 for a two-port DUT.
Understanding S-parameters in this manner can be misleading, as these definitions are not practical in reality. For example, even hobbyist VNAs, like the NanoVNA, show a diagram on the backplate with a definition of S-parameters that assumes the incident wave of the second port is zero. Of course, it is best to design things to be as well-matched as possible, but there will come a point (i.e., frequency) where achieving perfect matching is simply not possible.
 Fig. 2. NanoVNA backplate diagram of measurement concept.
Fig. 2. NanoVNA backplate diagram of measurement concept.
The reflection you see at the non-driving port is what we refer to as the switch term. The name can be misleading, as we have not yet discussed switches. However, there is a reason why we call this phenomenon switch term. The key point for you to understand is that the incident wave of the non-driving port is directly related to the switch term.
The name “switch term” comes from how VNAs are commonly made. In many VNAs, an electronic switch flips between the ports to drive each port. When one port is in driving mode, the other ports are terminated. Usually, the termination is part of the switch itself. Therefore, because the reflection is the result of a mismatch in termination of the non-driving ports, name “switch term” was coined for this reflection. You can read more about the origin of this name from [2].
The illustration below shows the two most common VNA architecture designs. On the left is the three-sampler approach, where a common receiver is used to sample the incident wave of the source and two receivers for reflections. The three-sampler design is often used in low-cost VNAs and in older designs. However, most new VNAs use a four-sampler design, where every port gets two receivers. With a four-sampler VNA, we can sample the incident wave of the source and termination (i.e., switch term). Keep in mind that for an N-port VNA, there are N switch terms.
Direct Measurement
In the following discussion, I will explain how S-parameters are defined and how switch terms arise. I will focus on two-port VNAs, but will provide the equation for N-port VNAs at the end.
In a two-port VNA, waves are sampled twice: once in the forward direction, driven by port-1, and once in the reverse direction, driven by port-2. Therefore, we have two sets of equations:
\[\begin{bmatrix} \hat{b}_{11}\\\hat{b}_{21} \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix}\begin{bmatrix} \hat{a}_{11}\\\hat{a}_{21} \end{bmatrix}, \qquad \begin{bmatrix} \hat{b}_{12}\\\hat{b}_{22} \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix}\begin{bmatrix} \hat{a}_{12}\\\hat{a}_{22} \end{bmatrix} \label{eq:4}\]where $\hat{a}_{ij}$ and $\hat{b}_{ij}$ represent the sampled incident and reflected waves, respectively, at port-i when driven by port-j. In the above notation, the S-parameters are the same whether the VNA is driving from port-1 or port-2, as the DUT remains constant. We can combine both results into a single matrix:
\[\begin{bmatrix} \hat{b}_{11} & \hat{b}_{12}\\ \hat{b}_{21} & \hat{b}_{22} \end{bmatrix} = \underbrace{\begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix}}_{\bs{S}}\begin{bmatrix} \hat{a}_{11} & \hat{a}_{12}\\ \hat{a}_{21} & \hat{a}_{22} \end{bmatrix} \label{eq:5}\]The above expression presents the correct way to calculate S-parameters. If you are using a four-sampler VNA, you can measure all eight waves. Therefore, you can simply take the inverse of the matrix containing the incident waves to obtain the S-parameters. The definition presented here already accounts for switch terms and can be extended to any number of ports.
Let’s go back to the topic of switch terms. They are still relevant, mainly because most VNA vendors offer four receivers in their two-port VNAs, but will still only use three of them and intentionally not sample the incident wave of the non-driving port. Why? I don’t know, maybe to maintain backward compatibility with old VNAs that actually only have three receivers. The most reasonable argument is to save buffer memory since fewer receivers mean less memory to use. This is not to say that the VNA will never use the fourth receiver, but it will only use it once to measure the switch terms, which are deterministic and part of the calibration procedure.
In a three-sampler VNA, the waves $\hat{a}_{12}$ and $\hat{a}_{21}$ are not measured due to a lack of dedicated receivers. In a four-sampler VNA, they are intentionally not measured. To address this, the matrix of measured incident waves in the above equation can be split into two matrices, as shown below:
\[\begin{bmatrix} \hat{b}_{11} & \hat{b}_{12}\\ \hat{b}_{21} & \hat{b}_{22} \end{bmatrix} = \bs{S}\begin{bmatrix} 1 & \frac{\hat{a}_{12}}{\hat{a}_{22}}\\ \frac{\hat{a}_{21}}{\hat{a}_{11}} & 1 \end{bmatrix}\begin{bmatrix} \hat{a}_{11} & 0\\ 0 & \hat{a}_{22} \end{bmatrix} \label{eq:6}\]Now, by taking the inverse of the diagonal matrix on the right-hand side, we obtain the ratios as below:
\[\begin{bmatrix} \frac{\hat{b}_{11}}{\hat{a}_{11}} & \frac{\hat{b}_{12}}{\hat{a}_{22}}\\ \frac{\hat{b}_{21}}{\hat{a}_{11}} & \frac{\hat{b}_{22}}{\hat{a}_{22}} \end{bmatrix} = \bs{S}\begin{bmatrix} 1 & \frac{\hat{a}_{12}}{\hat{a}_{22}}\\ \frac{\hat{a}_{21}}{\hat{a}_{11}} & 1 \end{bmatrix} \label{eq:7}\]So now, we define the ratios on the left-hand side of the above equation as the measured S-parameters (this is just a definition). We can then rewrite the remaining ratios on the right-hand side as follows:
\[\begin{bmatrix} \overbar{S}_{11} & \overbar{S}_{12}\\ \overbar{S}_{21} & \overbar{S}_{22} \end{bmatrix} = \bs{S}\begin{bmatrix} 1 & \overbar{S}_{12}\Gamma_{12}\\ \overbar{S}_{21}\Gamma_{21} & 1 \end{bmatrix} \label{eq:8}\]where $\overbar{S}_{ij}$ represents the measured S-parameters and $\Gamma_{ij}$ represents the switch terms:
\[\overbar{S}_{ij} \stackrel{\text{def}}{=} \frac{\hat{b}_{ij}}{\hat{a}_{jj}}, \qquad \Gamma_{ij} \stackrel{\text{def}}{=} \frac{\hat{a}_{ij}}{\hat{b}_{ij}} \label{eq:9}\]The switch terms are formed by the ratios of the receivers of the non-driving port. Therefore, they are independent of the measured DUT, as any influence by the DUT will be seen equally by both waves $\hat{a}_{ij}$ and $\hat{b}_{ij}$. In general, the S-parameters corrected for switch terms are given as follows:
\[\bs{S} = \begin{bmatrix} \overbar{S}_{11} & \overbar{S}_{12}\\ \overbar{S}_{21} & \overbar{S}_{22} \end{bmatrix}\begin{bmatrix} 1 & \overbar{S}_{12}\Gamma_{12}\\ \overbar{S}_{21}\Gamma_{21} & 1 \end{bmatrix}^{-1} \label{eq:10}\]In the special case where the measured two-port device is transmissionless, the switch terms $\Gamma_{ij}$ have no influence because $\overbar{S}_{21}=\overbar{S}_{12}=0$. In a four-sampler VNA, we can directly measure $\Gamma_{ij}$ by connecting any transmissive device and calculating the ratio according to the definition in \eqref{eq:9}. Note that switch terms are deterministic and can be measured once and reused. Therefore, after computing $\Gamma_{ij}$, you no longer need to use the fourth receiver since $\overbar{S}_{ij}$ can be measured using only three receivers.
Fun fact: The S-parameters measured with most VNAs are, to my knowledge, always defined as ratios, even when this is not the correct definition, as the incident wave of the non-driving port is not zero. This definition is only valid for single port devices. The reason why VNA vendors do this goes back to the reason why they intentionally don’t sample the fourth receiver.
For completeness, below is the structure of switch term corrected N-port S-parameter measurements:
\[\bs{S} = \begin{bmatrix} \overbar{S}_{11} & \overbar{S}_{12} & \overbar{S}_{13} & \cdots &\overbar{S}_{1N} \\ \overbar{S}_{21} & \overbar{S}_{22} & \overbar{S}_{23} & \cdots & \overbar{S}_{2N} \\ \overbar{S}_{31} & \overbar{S}_{32} & \overbar{S}_{33} & \cdots & \overbar{S}_{3N} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ \overbar{S}_{N1} & \overbar{S}_{N2} & \overbar{S}_{N3} & \cdots & \overbar{S}_{NN} \end{bmatrix}\begin{bmatrix} 1 & \overbar{S}_{12}\Gamma_{12} & \overbar{S}_{13}\Gamma_{13} & \cdots &\overbar{S}_{1N}\Gamma_{1N} \\ \overbar{S}_{21}\Gamma_{21} & 1 & \overbar{S}_{23}\Gamma_{23} & \cdots & \overbar{S}_{2N}\Gamma_{2N} \\ \overbar{S}_{31}\Gamma_{31} & \overbar{S}_{32}\Gamma_{32} & 1 & \cdots & \overbar{S}_{3N}\Gamma_{3N} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ \overbar{S}_{N1}\Gamma_{N1} & \overbar{S}_{N2}\Gamma_{N2} & \overbar{S}_{N3}\Gamma_{N3} & \cdots & 1 \end{bmatrix}^{-1} \label{eq:11}\]While there may seem to be a lot of switch terms, there are actually only N unique switch terms. This is because all switch terms in the same matrix row are equal. Since there are N rows, there are N switch terms.
\[\Gamma_{ij} = \Gamma_{ik}, \qquad \text{for all } j\ne k \label{eq:12}\]The reason why switch terms are the same regardless of the excited port is due to the fact that they are reflections caused by physical objects. They are the reflection of the termination load of the port. As long as the termination is not changed during the switching between ports, the switch terms remain the same regardless of the driving port.
Indirect Measurement
Below, I present a new method for indirectly measuring switch terms [1]. This method uses only three receivers of the VNA and a couple of reciprocal devices.
To begin the derivation, we describe a two-port measurement using T-parameters. By defining T-parameters using wave quantities, we arrive at two equations: one for the forward direction and the other for the reverse direction.
\[\begin{bmatrix} \hat{a}_{11}\\\hat{b}_{11} \end{bmatrix} = \begin{bmatrix} T_{11} & T_{12}\\ T_{21} & T_{22} \end{bmatrix}\begin{bmatrix} \hat{a}_{21}\\\hat{b}_{21} \end{bmatrix}, \qquad \begin{bmatrix} \hat{a}_{12}\\\hat{b}_{12} \end{bmatrix} = \begin{bmatrix} T_{11} & T_{12}\\ T_{21} & T_{22} \end{bmatrix}\begin{bmatrix} \hat{a}_{22}\\\hat{b}_{22} \end{bmatrix} \label{eq:13}\]By combining both results into a single matrix, we get the following:
\[\begin{bmatrix} \hat{a}_{11} & \hat{a}_{12}\\ \hat{b}_{11} & \hat{b}_{12} \end{bmatrix} = \underbrace{\begin{bmatrix} T_{11} & T_{12}\\ T_{21} & T_{22} \end{bmatrix}}_{\bs{T}}\begin{bmatrix} \hat{a}_{21} & \hat{a}_{22}\\ \hat{b}_{21} & \hat{b}_{22} \end{bmatrix} \label{eq:14}\]Now, let’s consider the error box model of a two-port VNA, as depicted in the illustration below. We can replace the matrix $\bs{T}$ in the above equation with the cascade model of the error box model, which gives us the following result:
\[\begin{bmatrix} \hat{a}_{11} & \hat{a}_{12}\\ \hat{b}_{11} & \hat{b}_{12} \end{bmatrix} = \bs{E}_\mathrm{L}\bs{T}_\mathrm{D}\bs{E}_\mathrm{R}\begin{bmatrix} \hat{a}_{21} & \hat{a}_{22}\\ \hat{b}_{21} & \hat{b}_{22} \end{bmatrix} \label{eq:15}\]where $\bs{E}_\mathrm{L}$ and $\bs{E}_\mathrm{R}$ are the left and right error boxes, and $\bs{T}_\mathrm{D}$ is the actual DUT.
 Fig. 4. Error box model of a two-port VNA.
Fig. 4. Error box model of a two-port VNA.
As the next step, the wave parameter matrices in the above equation are split into two parts: a diagonal part and a non-diagonal part.
\[\begin{bmatrix} 1 & \frac{\hat{a}_{12}}{\hat{b}_{12}}\\ \frac{\hat{b}_{11}}{\hat{a}_{11}} & 1 \end{bmatrix}\begin{bmatrix} \hat{a}_{11} & 0\\ 0 & \hat{b}_{12} \end{bmatrix} = \bs{E}_\mathrm{L}\bs{T}_\mathrm{D}\bs{E}_\mathrm{R}\begin{bmatrix} \frac{\hat{a}_{21}}{\hat{b}_{21}} & 1\\ 1 & \frac{\hat{b}_{22}}{\hat{a}_{22}} \end{bmatrix}\begin{bmatrix} \hat{b}_{21} & 0\\ 0 & \hat{a}_{22} \end{bmatrix} \label{eq:16}\]The above expression can be further simplified by multiplying the inverse of the diagonal matrix at the right-hand side. This reduces all wave parameters into ratios, as given below:
\[\begin{bmatrix} 1 & \frac{\hat{a}_{12}}{\hat{b}_{12}}\\ \frac{\hat{b}_{11}}{\hat{a}_{11}} & 1 \end{bmatrix}\begin{bmatrix} \frac{\hat{a}_{11}}{\hat{b}_{21}} & 0\\ 0 & \frac{\hat{b}_{12}}{\hat{a}_{22}} \end{bmatrix} = \bs{E}_\mathrm{L}\bs{T}_\mathrm{D}\bs{E}_\mathrm{R}\begin{bmatrix} \frac{\hat{a}_{21}}{\hat{b}_{21}} & 1\\ 1 & \frac{\hat{b}_{22}}{\hat{a}_{22}} \end{bmatrix} \label{eq:17}\]The final simplification is to replace the ratios with the definitions established in \eqref{eq:9}. This yields the following expression:
\[\begin{bmatrix} 1 & \Gamma_{12}\\ \overbar{S}_{11} & 1 \end{bmatrix}\begin{bmatrix} 1/\overbar{S}_{21} & 0\\ 0 & \overbar{S}_{12} \end{bmatrix} = \bs{E}_\mathrm{L}\bs{T}_\mathrm{D}\bs{E}_\mathrm{R}\begin{bmatrix} \Gamma_{21} & 1\\ 1 & \overbar{S}_{22} \end{bmatrix} \label{eq:18}\]Our goal is to extract $\Gamma_{21}$ and $\Gamma_{12}$ without prior knowledge of the error boxes or the DUT. We can do this by assuming that the DUT is a reciprocal device, which has the property of $\mathrm{det}\left(\bs{T}_\mathrm{D}\right)=1$. By applying the determinate operator to \eqref{eq:18} and using the determinate property $\mathrm{det}\left(\bs{A}\bs{B}\right)=\mathrm{det}\left(\bs{A}\right)\mathrm{det}\left(\bs{B}\right)$, we arrive at the following expression:
\[(1-\overbar{S}_{11}\Gamma_{12})\frac{\overbar{S}_{12}}{\overbar{S}_{21}} = \underbrace{\mathrm{det}\left(\bs{E}_\mathrm{L}\right)\mathrm{det}\left(\bs{E}_\mathrm{R}\right)}_{c}(\Gamma_{21}\overbar{S}_{22}-1) \label{eq:19}\]The above expression can be simplified as follows:
\[\frac{\overbar{S}_{12}}{\overbar{S}_{21}}-\overbar{S}_{11}\frac{\overbar{S}_{12}}{\overbar{S}_{21}}\Gamma_{12} -\overbar{S}_{22}c\Gamma_{21} + c = 0 \label{eq:20}\]From above equation we can see that we have a linear equation in three unknowns: $\Gamma_{12}$, $c\Gamma_{21}$, and $c$. Therefore, if we measure at least three unique transmissive reciprocal devices, we can solve for these unknowns by solving the following linear system of equations:
\[\begin{bmatrix} -\overbar{S}_{11}^{(1)}\frac{\overbar{S}_{12}^{(1)}}{\overbar{S}_{21}^{(1)}} & -\overbar{S}_{22}^{(1)} & 1 & \frac{\overbar{S}_{12}^{(1)}}{\overbar{S}_{21}^{(1)}}\\ \vdots & \vdots & \vdots & \vdots\\ -\overbar{S}_{11}^{(M)}\frac{\overbar{S}_{12}^{(M)}}{\overbar{S}_{21}^{(M)}} & -\overbar{S}_{22}^{(M)} & 1 & \frac{\overbar{S}_{12}^{(M)}}{\overbar{S}_{21}^{(M)}} \end{bmatrix}\begin{bmatrix} \Gamma_{12}\\ c\Gamma_{21}\\ c\\ 1 \end{bmatrix} = \bs{0} \label{eq:21}\]Here, $M\geq 3$ represents the number of measured reciprocal devices. We need at least three unique measurements to solve for the unknowns, as the system matrix must have a rank of 3 to be solvable. To solve for the unknowns, we must find the nullspace of the system matrix. This can be computed through singular value decomposition (SVD), where the best approximation of the nullspace corresponds to the right singular vector that corresponds to the smallest singular value. Since the nullspace is only unique up to a scalar multiple, we can solve for the switch terms by taking the ratio of the elements of the nullspace vector as follows:
\[\Gamma_{12} = \frac{v_{41}}{v_{44}}, \qquad \Gamma_{21} = \frac{v_{42}}{v_{43}} \label{eq:22}\]where $\bs{v}_{4} = [v_{41}, v_{42}, v_{43}, v_{44}]^T$ is the nullspace vector found through the SVD.
When selecting reciprocal devices, there are a few things to keep in mind. First, remember that we can only solve for the switch terms if the system matrix above has sufficient rank. If you choose devices that have similar frequency responses, you will get a poor estimation of the switch terms. For instance, it’s not advisable to use two transmission lines, as they may have similar phase at certain frequencies. Instead, opt for series resistive loads, which are reciprocal and have dissimilar frequency responses. You can use one thru and two series resistors (e.g., 50 and 100 ohm). Don’t be concerned about the frequency response of the resistors not being ideal, as long as they are different and reciprocal (transmissive), it should work.
You can check my GitHub repository for measurements and comparisons between the direct and indirect methods of measuring switch terms: https://github.com/ZiadHatab/vna-switch-terms
References
[1] Z. Hatab, M. E. Gadringer and W. Bösch, “Indirect Measurement of Switch Terms of a Vector Network Analyzer with Reciprocal Devices,” in IEEE Microwave and Wireless Technology Letters, 2023, doi: 10.1109/LMWT.2023.3311032, e-print doi: 10.48550/arXiv.2306.07066.
[2] R. B. Marks, “Formulations of the Basic Vector Network Analyzer Error Model including Switch-Terms,” 50th ARFTG Conference Digest, 1997, pp. 115-126, doi: 10.1109/ARFTG.1997.327265.